What is MFI (Mean or Median Fluorescence Intensity) and how do I calculate it in FCS Express?
What is MFI?
The term, MFI, is used commonly within the flow cytometry community. However, it does not have a universal meaning, and it is incumbent upon the researcher or scientist to define it.
MFI refers to the Mean, or Median, Fluorescence Intensity. In FCS Express, you may select three statistics to represent MFI for your data.
- Arithmetic mean, or Average, is the sum of N numbers divided by N.
- Geometric mean is the Nth root of the product of N numbers.
- Median, which is the 50th percentile of a population, represents the value at which half of a measured population is above and the other half below.
Using Statistics in FCS Express to report MFI
Once you have determined the appropriate statistic for MFI in your study, you can insert a statistics table to display the statistics of interest. Simply right click on a plot and choose the appropriate option to insert either Histogram Statistics, Gate Statistics, or Quadrant Statistics. Additionally, integrated spreadsheets may be used to report MFI values.
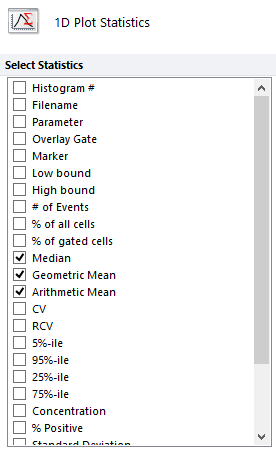
For univariate (1D) plots, such as histograms, you can choose to display either the Arithmetic Mean, the Geometric Mean, or the Median, for the X axis parameter.
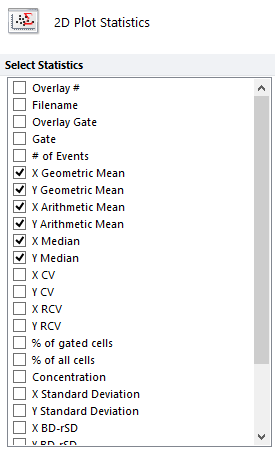
For bivariate (2D) plots, you can select X Geometric Mean, Y Geometric Mean, X Arithmetic Mean, Y Arithmetic Mean, X Median, and Y Median, where X and Y represent the X and Y parameters which are being displayed in the 2D plot of interest.
These statistical tables can be formatted rather easily, by right clicking on the table and choosing the statistics of interest, or, by formatting the table.
Spreadsheets and tokens can also be inserted in the analysis to quickly show a statistic of interest.
Tokens are dynamic text that update in real time. Tokens can be inserted in text boxes within an FCS Express analysis, or placed within a spreadsheet, and can represent a statistic, keyword, or properties of the layout, among other bits of information regarding the analysis.
Cautions
- While the Mean might be most useful when used to describe normal distributions and not bi-modal or multi-modal data, the Median is a non-parametric statistic in that it is a better indicator of the central tendency of your data, regardless of the underlying data distribution.
- The Arithmetic Mean is affected by outliers, while the Median is less sensitive to outliers.
- In general, the geometric mean statistic is only useful for positive values.
- This especially applies to digital FCS 3.x flow cytometry data.
- In FCS Express, if a population contains any events that have a negative raw value, FCS Express will display the geometric mean for that population:
- as N/A in a statistics table,
- or as ##ERROR## when a token is used to represent that statistic.
- Scaling choices will impact how the data is presented visually on the plot, but will not affect the statistical value.
