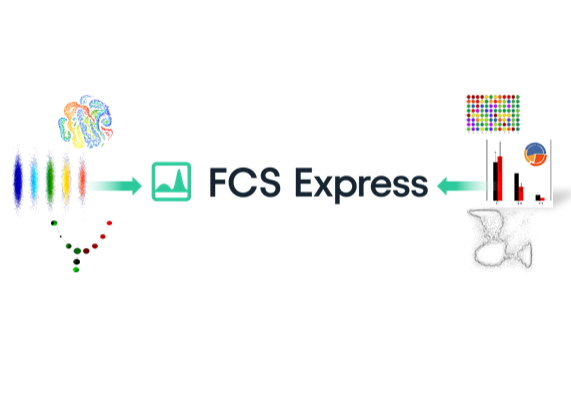
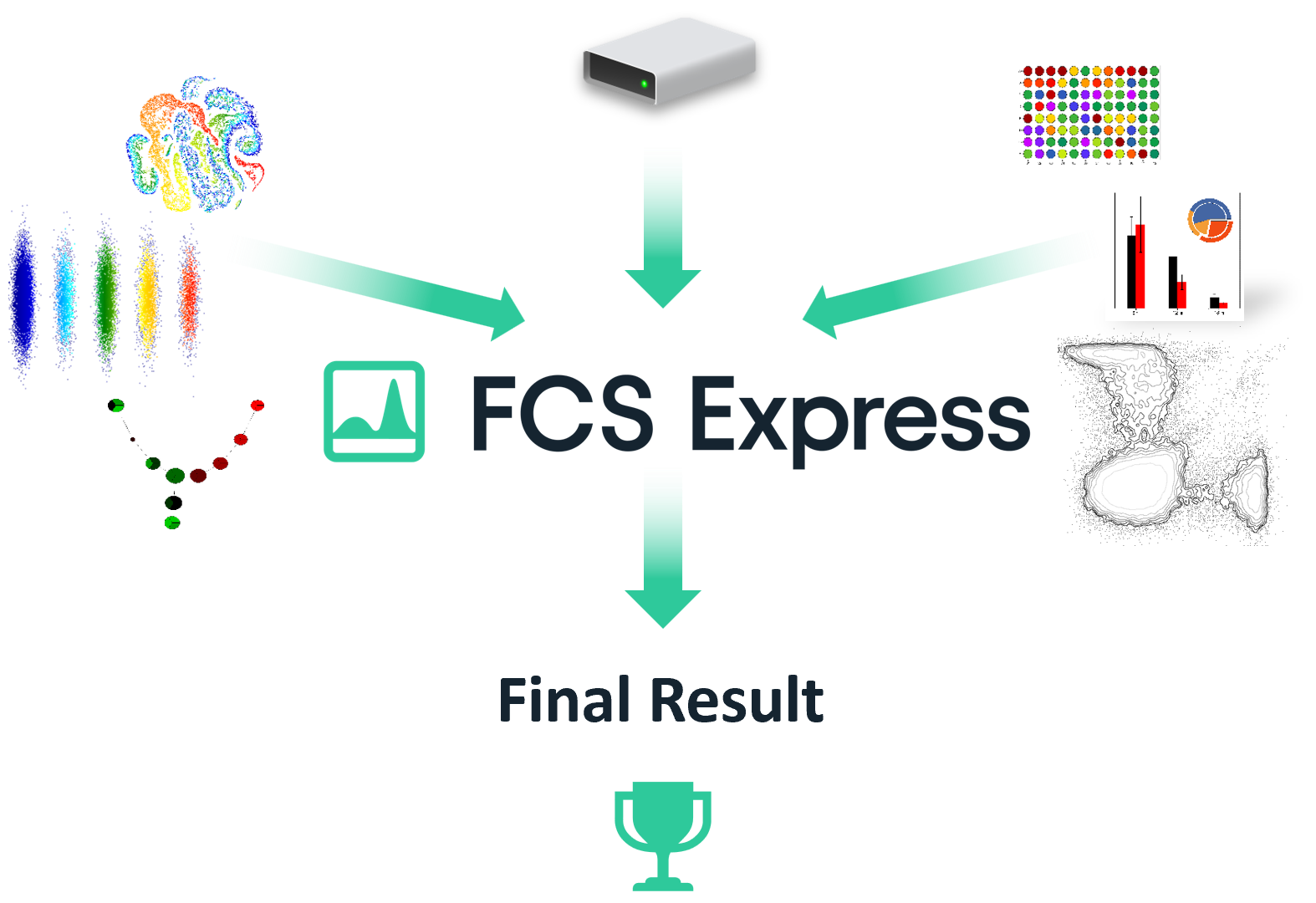
Bridging The Gap Between Flow Cytometry and Results
FCS Express™ gets you from raw data to easily-understandable, beautifully formatted, presentation-ready results more easily and in less time than any other flow cytometry software.
FCS Express is trusted by thousands of researchers around the world
Academic/Corporate R&D
Go from raw cytometry data to clearly communicated answers quickly, confidently, and easily
Individual researchers, shared resources facilities, and R&D start here!
Validation Ready Package
Assembled to help researchers meet their demanding GxP needs and requirements.
Cell and Gene Therapy Researchers Start Here!
Clinical and Diagnostic
See why FCS Express is the most widely used flow cytometry data analysis software among clinical labs
Clinical Diagnostic and Clinical Reference Labs start here!
Want to Learn FCS Express? You've Already Started!
Know how to use Microsoft PowerPoint™? How about Excel™?
Learning how to use flow cytometry software should not be an impediment to getting results from your data. FCS Express is designed to look, feel, and work like many familiar Microsoft Office™ programs so you are already half way to being an expert with the software before you even get started.

Making the switch from FlowJo™ to FCS Express?
If you are currently using FlowJo and are having trouble arriving at publication quality results, find it hard learning an unfamiliar software interface, find yourself constantly having to copy and paste tables and graphics to other software packages, then FCS Express might be just what you are looking for!
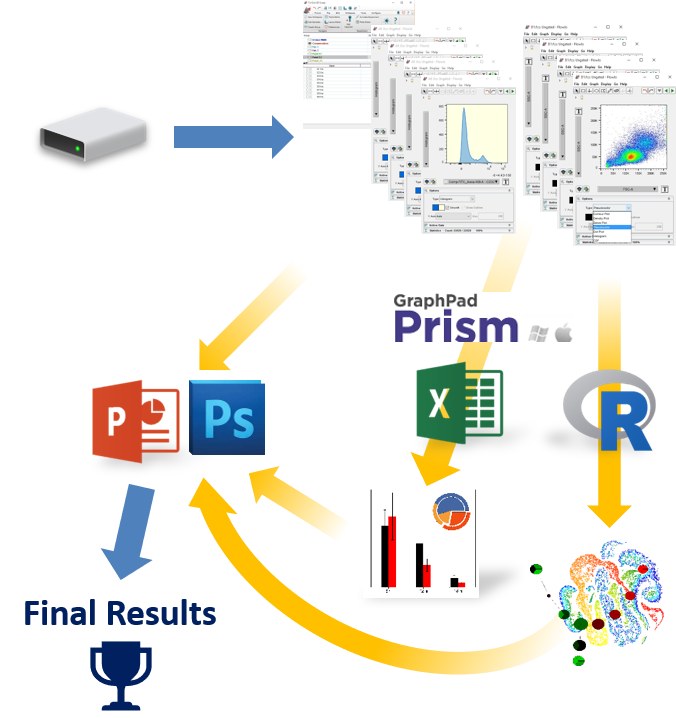
Integrated Spreadsheets Make Analysis Easy
Imagine having the power of Excel with results linked directly to your gates. With FCS Express spreadsheets can be accessed directly in your analysis and linked up to your gates and data files. As gates move and data changes, so do your spreadsheets in real time. Say good bye to copy and paste and hello to results!
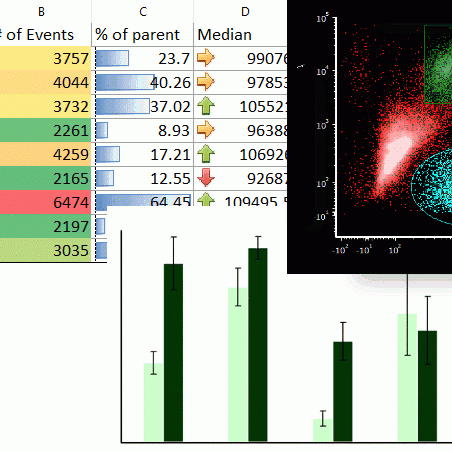
Testimonials
"FCS Express has revolutionized the way we think about data analysis. Not only are ALL the analysis tools available at your fingertips, the ability to work in a “Microsoft-like” environment makes the whole process intuitive and a great time savings. Our users have shared the same level of enthusiasm about our decision to switch to FCS Express for all our data analysis needs.”
Joanne Lannigan Ph.D.
Director, Flow Cytometry Core
University of Virginia
School of Medicine
"FCS Express is the most intuitive, flexible, and comprehensive flow cytometry software we have ever used. The company is extremely responsive and supportive with helping us to accomplish very complex analyses and make sure the software is meeting our clinical laboratory needs. We have gone through several instrument and LIS transitions over the past 10 years and have been able to rely on the software to help alleviate the pain of those changes. We would highly recommend this for any flow lab!"
Carrie Gifford
Business Manager, Cancer & Blood Diseases Institute
Clinical Laboratories
“FCS express is a much better program than my good old go to Flow Jo. The support is amazing, as typically taken care of immediately, and honestly 24 hours is the typical. Flow Jo has great webinars, but FCS Express has a bunch of webinars as well, and again cannot beat the technical support. So glad I was put into a position where I needed to leave my traditional go to [FlowJo], as FCS express has won me over. Still new so may still have questions but love it so far.”
Karen F. Underwood, MS
Research Lead Specialist
University of Maryland Greenebaum Comprehensive Cancer Center Flow Cytometry Services
"I am a big fan of FCS Express, it's the first tool I used to analyze flow data and I absolutely love it! Thank you for building that wonderful tool! It helped me get my Masters and also get 6 papers published”
Abhijith Segu SCYM(ASCP)
Senior Research Associate
R&D
Bioqual
"The customer service, and the functionality of the software is by far the best I’ve seen. Unless forced to, I will never touch FlowJo again"
-Anonymous
"You guys have the best customer service of ANY product I own."
David Grier
Wake Forest School of Medicine
"My users love the interface of FCS Express and find it quick and easy to learn. We love the speed and flexibility with data analysis. As a core manager, I appreciate the support the FCS Express team provides; they are always available to help my users."
Vanessa Scarfone
Flow Cytometry Core Manager
Stem Cell Research Center
University of California Irvine
"Our group uses a wide variety of software for data analysis and processing. We are committed to using FCS express for our flow cytometry data needs as it is the most intuitive and flexible software available. The ease in interfacing with other Windows-based software and a convenient multiuser network installations were major determinants in our decision to purchase FCS Express. My staff enjoys being able to log in and process data from any desktop computing system in our facility. Application support and accessibility to a network of FCS Express users has also been very useful in developing batch processing and production protocols. Overall, I have not experienced the ease of use and broad applicability with other flow software product."
David DiGiusto, PhD
"I have found the online support material has been really helpful to my students to extend their knowledge independently."
Terry Pinfold
Cytometry and Histology Lab Manager, University of Tasmania
"I can't say enough good things about the program and the people who work on it."
Lisa Kohli
Laboratory Technician
"My function here at Labcorp is to set up a work flow process for over 350 cases a day companywide so without a doubt I am choosing FCS Express to accomplish this. In my opinion there just isn't another software option for us. I need a user friendly package that will accommodate our current complex multicolor analysis as well as be able to expand for future growth, provide high quality reports for our clients, offer a virtual component for those customers that want to offer tech only flow or more closely interact with their patient results and the big challenge is that this has to happen in an extremely high volume reference laboratory. De Novo Software has been able to provide us with the features that we need and their technical support is extraordinary. I can't imagine a successful clinical lab without FCS Express; it is the "go-to" Clinical package."
Horacio Vall CLS, SCYM(ASCP)
Vice-President Science & Technology
Doctor of Biochemistry
Flow Cytometry Discipline Director Laboratory Corporation of America Holdings
"A major decision in our choice of software packages was dictated by how well we thought it would integrate with our report writing software (MS Word.) It is my impression that FCS Express does a better job with interfacing with other widely used software programs than the two other programs that we evaluated. It is hard to put into words, but FCS Express also seemed to have the look and feel of what I thought a "clinical" software program should be. Currently we spend excessive time in clerical tasks of transferring numerical values into our reports. In comparison with the other programs we reviewed, FCS Express seems to better suited to handle these repetitious tasks that are a big part of our clinical work and help separate this application from the needs of a "research" user. In short, the "automation" features of FCS Express seem stronger which are important to our clinical laboratory. Currently there is a labor tight market for qualified personnel in our area and we find it hard to attract technicians. Moreover it often takes years to fully train a technician. By using FCS Express anticipate shortening the training cycle by allowing our technicians more time to focus on the more demanding tasks in flow cytometry and less on clerical busy work. We are currently using DiVa, which is a great data acquisition program, but it does have serious limitations when used for routine data analysis and report generation thus leading to our decision to purchase FCS Express."
Nick Gonchoroff
Retired Associate Professor
Suny-Upstate Medical University
"The Hematopathology laboratory of the Shands Hospital at the University of Florida analyzes numerous bone marrow, blood and lymphoid tissue samples for the diagnosis of leukemia, lymphoma and related neoplastic conditions every day. We have been using BD's software for our data acquisition and analysis for many years. While adequate for acquisition, this software has several limitations regarding data analysis that recently prompted us to look for alternative programs for our clinical analytical work. De Novo Software has provided an analysis tool that is completely optimized for clinical laboratories like ours. Within a short period of time, we created a drastically improved analysis protocol in FCS Express and it seems that every day we discover new features, such as tokens, alerts, panels, etc. that easily allow us to improve the quality of the analysis. Above all, I am extremely impressed with the excellence of the support staff that is always available to answer questions and courteously and positively responds to suggestions. In my opinion, FCS Express is one of the best programs available today for clinical flow cytometry laboratories."
Raul Braylan
Former Medical Director, Flow Cytometry Laboratory of the Shands Teaching Hospital at the University of Florida
"I used to be in flowjo camp but I'm now totally converted to FCS express camp! Loving your software"
-Anonymous
"I am reaching out to let you know that V7 has been a great experience. My analysis time has been chopped by more than 50%. All the new features, etc, are great!"
Alberto Robert
Genetech
"Flow cytometry-based research was a large component of my graduate training as it is a superior approach for quantifying immune cell abundance & analyzing immune phenotypes at the protein level. At Roswell Park Comprehensive Cancer Center's Flow and Immune Analysis Shared Resource, we used FCS Express to study IRF8 protein expression in macrophages and monocytes within murine and human breast cancer models in our most recent publication. I truly appreciated the one-on-one training, program updates and friendly support from the De Novo Software team and we are proud to recommend FCS Express for flow cytometry data analysis."
Stephanie Tzetzo, PhD, MA
Department of Immunology
Roswell Park Comprehensive Cancer Center
What's New
WIKIS
*PowerPoint and Excel are trademarks of Microsoft Corporation | †R is a trademark of the R Foundation | ‡Prism is a trademark of GraphPad Software, Inc. | FlowJo is a trademark of Flowjo, LLC